线性代数与鸡兔同笼
线性代数很难学!
因为书真的很难懂。可能是数学家并不希望我们能和他们站在同一水平线上,他们讲出来的东西充满的黑话和切口;也可能是我还没学会、还没理解数学的精妙,所以无法理解…
我总怀疑是教育的问题
毕竟一切自己的无能都可以怪教育、怪家庭、怪党怪政府
矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合。
现代的线性代数教育都是这么开始的吧…… 这个定义是如此精妙,以至于几乎不包含什么有用的信息。好吧我知道$ \begin{matrix}1 & 2 \cr 3 & 4 \end{matrix} $这样是矩阵了,然后呢?
然后,讲课的白胡子老头就在黑板上多举几个例子,你慢慢想起了五行八卦、奇门遁甲、风水堪舆、封神演义…… 我擦嘞,这门课不会这么NB吧?
认真听课、认真听课!看看老神仙用矩阵干嘛。
然后!可但是! 转折出现了:老神仙老头说介玩意用来解方程组…… 你是不是有病?说好的封神演义呢?我想祭起一块金砖砸你你造吗?
然后,老头老家伙带着你解了无数的方程,系数都没超过过100,丫的竟然还是用高斯消元法!我本来就会好不好?你这样搞比直接解方程还麻烦了好不好?你就是有病!
然后就是标准的大学生学习方法:逃课、抄作业、考试周突击、放假忘光。
现在你都解释不清楚线性代数是干嘛用的吧?我就问你敢不敢说自己当年学过线性代数?
老神仙讲奇门遁甲的时候反正我是不在教室的……
矩阵是线性变换
逃了一些课之后,再去上课就像听天书了……全是没听过的咒语。只能无助地看着一堆 $ 1 2 3 4 5 $ 在黑板上各种变换。
把一些点变来变去又有什么用呢?结论还是:有病!所以,继续不上课。
昨天忽然想通了:运动是相对的。变换也可以是点不动,坐标系动;结果就可以得到不同坐标系下同一个点的向量表述。忽然就理解机器学习是在寻找什么了:用两种不同的语言,描述同一个东西,找到两种语言的翻译方法。描述用向量表示,翻译方法就是一个矩阵,翻译过程居然就是
$$ Ax=b$$
我擦嘞!老神仙第一天就讲了这个!忽然想哭有木有?
有监督的机器学习就是:给出一堆 $x \to b$ 的映射,让机器帮忙找到一个 $A$, 尽量满足所有的 $Ax=b$。然后再拿到新的 $x$ ,马上就可以做 $A \cdot x$, 得到相应的 $b$ 表述。
这玩意一点儿也不高深啊!怪不得科学家们都不说人话,一上来就和你谈使用贝叶斯的时候如何进行拉普拉斯平滑才能更好地…… 而且,顶尖科学家会在说明过程中向你投掷100个公式!完全无法一起开心地玩耍。
真的吗?
我也觉得这种理解太肤浅了!所以尝试用这个思想推导一下鸡兔同笼问题来验证。
因为线性空间要求实数域,我们假设鸡和兔兔的头和腿能被精确地分割成小数:半只鸡就一条腿、$\frac{1}{4}$只鸡就半条腿。嗯,没毛病。 额,还有负数只…… 就当欠别人吧。
对于一个给定的事实:一些鸡和兔兔们在一起,我们用两种视角去看待它:
$c$只鸡和$r$只兔兔在一起,我们(在鸡兔坐标系中)用$(c,r)$表示。如果我们用向量 $\binom{c}{r}$ 来表示这种描述,可以证明所有鸡兔数量的向量构成一个向量空间。 此处我们使用显然定理,哇哈哈哈~ 另外,它其实就是$R^2$。
$h$只头和$l$只腿腿在一起(好恐怖…),我们(在头腿坐标系中)用$(h,l)$表示。我们用向量 $\binom{h}{l}$ 来表示这种描述。
可以证明两种表述间存在一一对应关系,此处再次使用显然定理,哈哈哈~
另一个重要的事实是对于这一堆动物,不管从什么角度去观察,虽然得到的观察结果看上去可能很不相同,但它们描述的都是一个毫无差别的事情。这一堆里面有几只鸡几只兔子、有几个头几条腿、或者其它的特征,不因观察而变化。这和盒子里的半死不活猫不一样。
正向思考总是很容易
已知鸡兔数量求头和腿的线性变换很容易想出来:
$$ \begin{bmatrix} 1 & 1\cr 2 & 4\end{bmatrix} \cdot \binom{c}{r} = \binom{h}{l}$$
咱们把这个矩阵叫做 A。 $ A = \begin{bmatrix} 1 & 1\cr 2 & 4\end{bmatrix} $
逆向就不是那么容易了
前面的思考告诉我们这个变换是存在的,但想直接写出来并不是那么容易(其实也不难)。但线性代数告诉我们反向的变换就是 $A$ 的逆矩阵 $A^{-1}$。
既然现在不是上学了,那么显然是要用工具进行具体计算的, 于是:
$$ A^{-1} = \begin{bmatrix} 2 & -\frac{1}{2} \cr -1 & \frac{1}{2} \end{bmatrix}$$
我们验证一下,假设有5个头和14条腿:
$$ \begin{bmatrix} 2 & -\frac{1}{2} \cr -1 & \frac{1}{2} \end{bmatrix} \cdot \binom{5}{14} = \binom{3}{2}$$
现在不管多少的头配腿,只要放到式子里面一算,马上就知道鸡和兔兔数量啦!
哇!这招数好神奇
$$ \begin{bmatrix} 1 & 1\cr 2 & 4\end{bmatrix} \cdot \binom{c}{r} = \binom{h}{l}$$
其实吧…
$$ 就是这个 \begin{cases} x + y = 5 \cr 2x+4y=14\end{cases} $$
到头来还是在解方程组…
只要用这一个矩阵就可以直接搞定一切鸡兔同笼问题了!
–
另外:
乌龟和螃蟹在一个笼子里…
(螃蟹十足目哦~ 我开始就用8条腿算的…)
$$ \begin{bmatrix} \frac{5}{3} & -\frac{1}{6}\cr -\frac{2}{3} & \frac{1}{6}\end{bmatrix} \cdot \binom{头}{腿} = \binom{龟}{蟹}$$- 三头四腿地狱犬和双头八脚章鱼怪在一个笼子里 (如果不互相吃的话…)
$$ \begin{bmatrix} \frac{1}{2} & -\frac{1}{8}\cr -\frac{1}{4} & \frac{3}{16}\end{bmatrix} \cdot \binom{头}{腿} = \binom{地狱犬}{章鱼怪}$$ - 大师兄讨厌的百足千眼多目怪和二师兄喜欢的八足八眼蜘蛛精
$$ \begin{bmatrix} -\frac{1}{900} & \frac{1}{900}\cr \frac{5}{36} & -\frac{1}{72}\end{bmatrix} \cdot \binom{足}{眼} = \binom{多目怪}{蜘蛛精}$$
密集恐惧症要犯了!!!想一下就恶心,怪不得大师兄也受不鸟 进阶的:蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀。已知共有21只,有140条腿和24对翅。奥数解法是先把六条腿的当成一类,一共做两次鸡兔同笼方法解决。矩阵:
$$ \begin{bmatrix} -3 & \frac{1}{2} & 0\cr
-4 & \frac{1}{2} & 1 \cr
8 & -1 & -1 \end{bmatrix} \cdot \left(\begin{array}{}{头}\cr{腿}\cr{翅}\end{array}\right) = \left(\begin{array}{}{蜘蛛}\cr{蜻蜓}\cr{蝉}\end{array}\right)$$本题就:
$$ \begin{bmatrix} -3 & \frac{1}{2} & 0\cr
-4 & \frac{1}{2} & 1 \cr
8 & -1 & -1 \end{bmatrix} \cdot \left(\begin{array}{}{21}\cr{140}\cr{24}\end{array}\right) = \left(\begin{array}{}蜘蛛 & 7\cr蜻蜓 & 10 \cr蝉 & 4\end{array}\right)$$
然后我们来看看机器学习
先做个线性回归,可以看到训练效果很好,很快就收敛到可接受的程度。之后用了一些时间来解决小数点后好多位的问题,因为我设置的训练停止条件是误差为0。
线性回归: 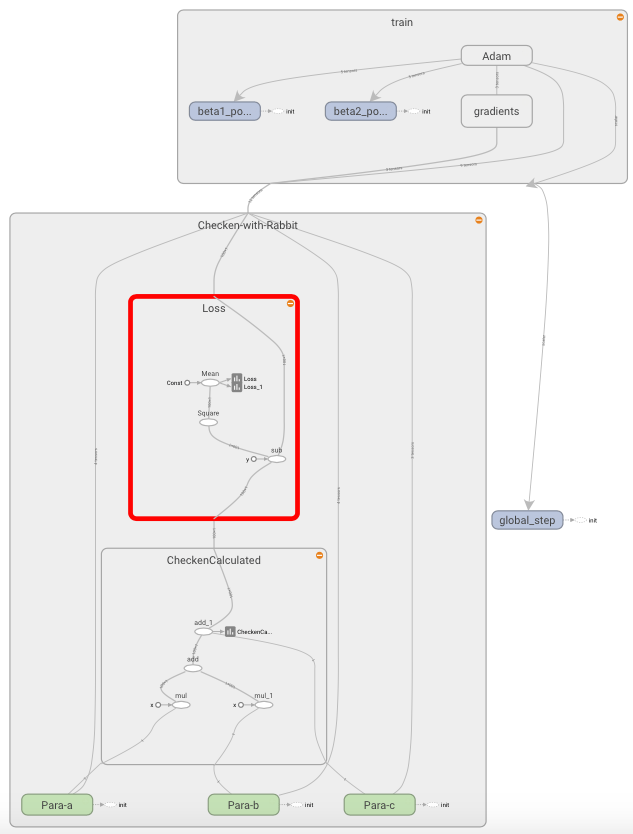
结果: 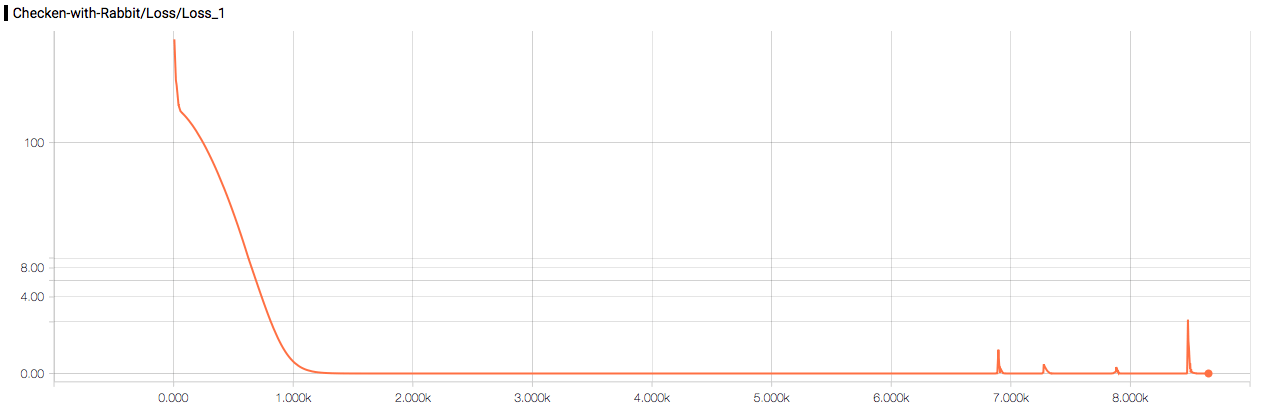
这只是验证一下,毕竟线性回归这种事情用 Excel 也能做
–
神经网络学习蜘蛛蜻蜓蝉哦: 
结果: 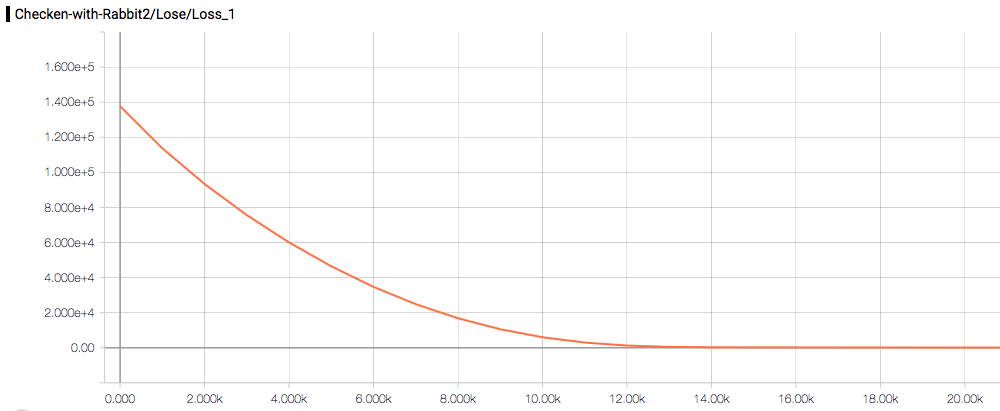
随便输出两条计算结果,已经很接近了。如果是求整数解,那就是正确的了: